Optimism & Base Chain L1 Data Fees
Understanding L1 Costs for L2 Calldata
I prefer to move calculations off-chain whenever possible to increase my ability to scale, and to decrease my latency.
More scale means more pairs, which means more opportunities to capture. And reduced latency often means the difference between a successful transaction and a reverted one.
Especially on fast chains like Arbitrum and Base!
You can’t manage highly concurrent Python code without a good understanding of latency and bottlenecks. Finding the balance is quite difficult — do everything yourself and risk drowning in complexity, or outsource everything and suffer from high latency and limited scale.
A bot can outsource nearly all of its work by sending RPC calls to a node, but this approach scales very poorly. A simple bot monitoring a few pairs can be built very quickly using this approach, but latency begins to compound exponentially once the number of pairs grows beyond that. Making more than a few on-chain calls is just too slow to reliably identify and secure opportunities.
To this end, most of the degenbot code base just replicates the on-chain behavior of popular DeFi contracts.
When I find myself calling a contract more than a few times, I get uneasy. I’ve been calling this one a lot lately:
We’ll come back to this soon.
What Is A Layer 2 Anyway?
Layer 2s are blockchains that are designed to work above and in parallel with another chain called a Layer 1. L2s typically have a limited peer-to-peer network, a centralized sequencer, and perhaps a small validator pool. L2s periodically post state updates to the L1 chain.
Much of how L2s operate is beyond the scope of this lesson, so I encourage you to read the Optimism documentation for more. Note that Base chain uses Optimism tech, so documentation for OP Mainnet applies to Base.
L1 Data Fees
When you interact with a L2 chain, you should know that it will record your activity back to L1.
Whenever you execute a L2 transaction, you pay twice:
The cost for including your transaction — this is the L2 execution fee.
The cost of recording the data back to L1 — this is the L1 data fee.
L1 data fees do not appear in transaction simulations, since they are paid during block inclusion at the sequencer. The fees are ultimately paid by the L2 when it submits an EIP-4844 blob or records the state directly on-chain via a normal transaction.
This fee mechanism is clearly explained in the Optimism documentation, but it’s not an obvious thing you would look for during your exploration of the chain. I was certainly surprised when my initial test transactions on Base had higher gas fees on-chain than those in the simulations.
Thus to successfully manage opportunities on an L2, you must track and account for both fee types. And given the popularity of L2s we can expect that the L1 data fee component to become more expensive.
L1 Data Fee Calculation
The set of standard Optimism contracts is available on GitHub in the contracts-bedrock directory of the optimism repository.
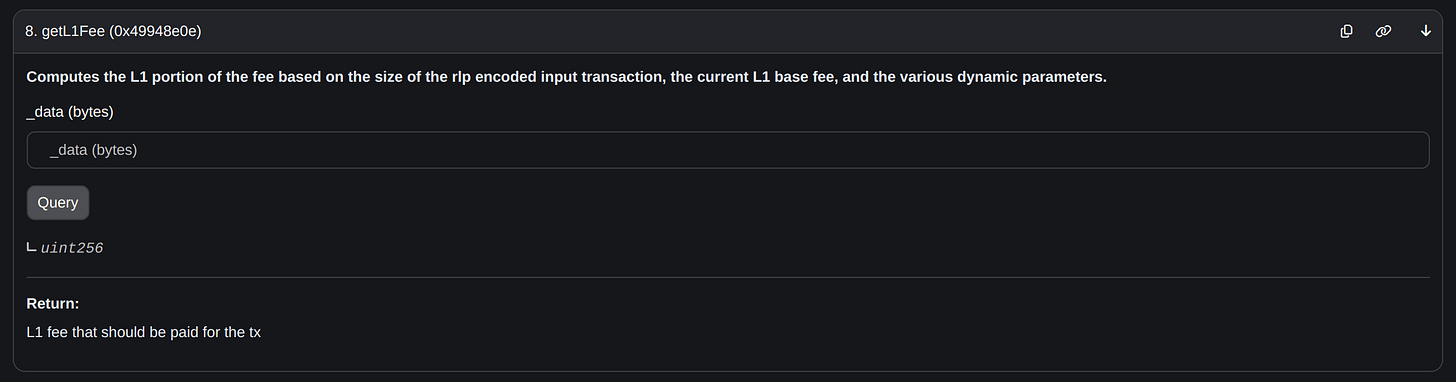
The GasPriceOracle.sol contract provides a function getL1Fee, which I clipped above:
/// @notice Computes the L1 portion of the fee based on the size of the
/// rlp encoded input transaction, the current L1 base fee, and the
/// various dynamic parameters.
/// @param _data Unsigned fully RLP-encoded transaction to get the L1
/// fee for.
/// @return L1 fee that should be paid for the tx
function getL1Fee(bytes memory _data) external view returns (uint256) {
if (isFjord) {
return _getL1FeeFjord(_data);
} else if (isEcotone) {
return _getL1FeeEcotone(_data);
}
return _getL1FeeBedrock(_data);
}Optimism regularly hardforks the network to perform protocol level changes, like Ethereum. The documentation includes all hardfork activations to date. The hardfork names are ordered alphabetically, beginning at Bedrock.
The L1 fee mechanism was first implemented in Bedrock, changed in Ecotone, and then again in Fjord. Fjord is relevant now, so it is the mechanism under consideration here. I will not cover the Bedrock or Ecotone versions.
GasPriceOracle.sol is a pre-deployed contract. The contract code for a pre-deploy is baked into the node software that operates the chain, and is available on the genesis block. This ensures that deployments of these contracts is always correct, and a botched deployment cannot harm the chain. It also ensures that chains using the Optimism structure have matching contracts.
GasPriceOracle.sol is an upgradable proxy contract at address 0x420000000000000000000000000000000000000F, currently pointing to 0xa919894851548179A0750865e7974DA599C0Fac7.
GasPriceOracle.sol
// SPDX-License-Identifier: MIT
pragma solidity 0.8.15;
import { ISemver } from "src/universal/ISemver.sol";
import { Predeploys } from "src/libraries/Predeploys.sol";
import { L1Block } from "src/L2/L1Block.sol";
import { Constants } from "src/libraries/Constants.sol";
import { LibZip } from "@solady/utils/LibZip.sol";
/// @custom:proxied
/// @custom:predeploy 0x420000000000000000000000000000000000000F
/// @title GasPriceOracle
/// @notice This contract maintains the variables responsible for
/// computing the L1 portion of the total fee charged on L2.
/// Before Bedrock, this contract held variables in state that were
/// read during the state transition function to compute the L1
/// portion of the transaction fee. After Bedrock, this contract now
/// simply proxies the L1Block contract, which has the values used
/// to compute the L1 portion of the fee in its state.
/// The contract exposes an API that is useful for knowing how large
/// the L1 portion of the
/// transaction fee will be. The following events were deprecated
/// with Bedrock:
/// - event OverheadUpdated(uint256 overhead);
/// - event ScalarUpdated(uint256 scalar);
/// - event DecimalsUpdated(uint256 decimals);
contract GasPriceOracle is ISemver {
...
}Calldata Compression
A key component of GasPriceOracle is LibZip.sol. LibZip is a byte compression library from the highly regarded Solady contracts.
Fjord chains post compressed transaction calldata to L1. Fjord L1 fee estimates work by passing the unsigned transaction through LibZip’s flzCompress function. Then the number of compressed bytes is used to estimate the L1 data cost.
Solady is highly optimized and makes heavy use of assembly blocks. flzCompress is written entirely in assembly:
/// @dev Returns the compressed `data`.
function flzCompress(bytes memory data) internal pure returns (bytes memory result) {
/// @solidity memory-safe-assembly
assembly {
function ms8(d_, v_) -> _d {
mstore8(d_, v_)
_d := add(d_, 1)
}
function u24(p_) -> _u {
_u := mload(p_)
_u := or(shl(16, byte(2, _u)), or(shl(8, byte(1, _u)), byte(0, _u)))
}
function cmp(p_, q_, e_) -> _l {
for { e_ := sub(e_, q_) } lt(_l, e_) { _l := add(_l, 1) } {
e_ := mul(iszero(byte(0, xor(mload(add(p_, _l)), mload(add(q_, _l))))), e_)
}
}
function literals(runs_, src_, dest_) -> _o {
for { _o := dest_ } iszero(lt(runs_, 0x20)) { runs_ := sub(runs_, 0x20) } {
mstore(ms8(_o, 31), mload(src_))
_o := add(_o, 0x21)
src_ := add(src_, 0x20)
}
if iszero(runs_) { leave }
mstore(ms8(_o, sub(runs_, 1)), mload(src_))
_o := add(1, add(_o, runs_))
}
function mt(l_, d_, o_) -> _o {
for { d_ := sub(d_, 1) } iszero(lt(l_, 263)) { l_ := sub(l_, 262) } {
o_ := ms8(ms8(ms8(o_, add(224, shr(8, d_))), 253), and(0xff, d_))
}
if iszero(lt(l_, 7)) {
_o := ms8(ms8(ms8(o_, add(224, shr(8, d_))), sub(l_, 7)), and(0xff, d_))
leave
}
_o := ms8(ms8(o_, add(shl(5, l_), shr(8, d_))), and(0xff, d_))
}
function setHash(i_, v_) {
let p_ := add(mload(0x40), shl(2, i_))
mstore(p_, xor(mload(p_), shl(224, xor(shr(224, mload(p_)), v_))))
}
function getHash(i_) -> _h {
_h := shr(224, mload(add(mload(0x40), shl(2, i_))))
}
function hash(v_) -> _r {
_r := and(shr(19, mul(2654435769, v_)), 0x1fff)
}
function setNextHash(ip_, ipStart_) -> _ip {
setHash(hash(u24(ip_)), sub(ip_, ipStart_))
_ip := add(ip_, 1)
}
result := mload(0x40)
calldatacopy(result, calldatasize(), 0x8000) // Zeroize the hashmap.
let op := add(result, 0x8000)
let a := add(data, 0x20)
let ipStart := a
let ipLimit := sub(add(ipStart, mload(data)), 13)
for { let ip := add(2, a) } lt(ip, ipLimit) {} {
let r := 0
let d := 0
for {} 1 {} {
let s := u24(ip)
let h := hash(s)
r := add(ipStart, getHash(h))
setHash(h, sub(ip, ipStart))
d := sub(ip, r)
if iszero(lt(ip, ipLimit)) { break }
ip := add(ip, 1)
if iszero(gt(d, 0x1fff)) { if eq(s, u24(r)) { break } }
}
if iszero(lt(ip, ipLimit)) { break }
ip := sub(ip, 1)
if gt(ip, a) { op := literals(sub(ip, a), a, op) }
let l := cmp(add(r, 3), add(ip, 3), add(ipLimit, 9))
op := mt(l, d, op)
ip := setNextHash(setNextHash(add(ip, l), ipStart), ipStart)
a := ip
}
// Copy the result to compact the memory, overwriting the hashmap.
let end := sub(literals(sub(add(ipStart, mload(data)), a), a, op), 0x7fe0)
let o := add(result, 0x20)
mstore(result, sub(end, o)) // Store the length.
for {} iszero(gt(o, end)) { o := add(o, 0x20) } { mstore(o, mload(add(o, 0x7fe0))) }
mstore(end, 0) // Zeroize the slot after the string.
mstore(0x40, add(end, 0x20)) // Allocate the memory.
}
}The function header gives a strong clue about flzCompress:
// LZ77 implementation based on FastLZ.
// Equivalent to level 1 compression and decompression at the following commit:
// https://github.com/ariya/FastLZ/commit/344eb4025f9ae866ebf7a2ec48850f7113a97a42
// Decompression is backwards compatible.It tells us that FastLZ is the algorithm being modeled by flzCompression. The FastLZ scheme and example C code is published on GitHub.
FastLZ
The FastLZ algorithm is quite straightforward. In compression mode, it operates over an input buffer, transforming duplicate byte chunks into a series of instructions.
In decompression mode, it operates on the encoded data, replaying the instructions to reconstruct the original data.
It has three instructions:
LITERAL RUN — Copy a consecutive run of 1 byte values from the input buffer to the output buffer
SHORT MATCH — Copy a consecutive run of 1 byte values from the output buffer to the end of the output buffer, starting at some offset
LONG MATCH — Copy a consecutive run of 1 byte values from the output buffer to the end of the output buffer, starting at some offset
The SHORT MATCH and LONG MATCH operate identically. The key difference is the length values that each can support.
SHORT MATCH is encoded into a 2 byte instruction, with 3 bits given to the length. The maximum 3 bit unsigned integer is 7. A match length of zero is nonsensical, so the length is offset so that 0 corresponds to a match length of 1.
LONG MATCH is encoded into a 3 byte instruction with 8 bits given to the length. The maximum 8 bit unsigned integer is 255. Again, a zero length is nonsensical, and matches up to 8 are supported by SHORT MATCH, so this value is offset such that 0 corresponds to a match length of 9.
Thus the maximum length supported by SHORT MATCH is 8 (7+1), and the maximum length supported by LONG MATCH is 262 (255+9).
LITERAL RUN provides 5 bits for its length. It is similarly offset so that a value of 0 indicates 1. Thus the maximum number of values supported by LITERAL RUN is 32 (31+1).
I encourage you to read the block format examples from the FastLZ repo, which includes several transformations that illustrate how the decompression method works.
Python Port
Solady provides a JavaScript library that replicates LibZip for offline testing.